Built-ins¶
The Agda type checker knows about, and has special treatment for, a number of
different concepts. The most prominent is natural numbers, which has a special
representation as Haskell integers and support for fast arithmetic. The surface
syntax of these concepts are not fixed, however, so in order to use the special
treatment of natural numbers (say) you define an appropriate data type and then
bind that type to the natural number concept using a BUILTIN pragma.
Some built-in types support primitive functions that have no corresponding Agda
definition. These functions are declared using the primitive keyword by
giving their type signature.
Using the built-in types¶
While it is possible to define your own versions of the built-in types and bind
them using BUILTIN pragmas, it is recommended to use the definitions in the
Agda.Builtin modules. These modules are installed when you install Agda and
so are always available. For instance, built-in natural numbers are defined in
Agda.Builtin.Nat. The standard library and the agda-prelude
reexport the definitions from these modules.
The unit type¶
module Agda.Builtin.Unit
The unit type is bound to the built-in UNIT as follows:
record ⊤ : Set where
{-# BUILTIN UNIT ⊤ #-}
Agda needs to know about the unit type since some of the primitive operations in the reflected type checking monad return values in the unit type.
The Σ-type¶
module Agda.Builtin.Sigma
The built-in Σ-type of dependent pairs is defined as follows:
record Σ {a b} (A : Set a) (B : A → Set b) : Set (a ⊔ b) where
constructor _,_
field
fst : A
snd : B fst
open Σ public
infixr 4 _,_
{-# BUILTIN SIGMA Σ #-}
Lists¶
module Agda.Builtin.List
Built-in lists are bound using the LIST built-in:
data List {a} (A : Set a) : Set a where
[] : List A
_∷_ : (x : A) (xs : List A) → List A
{-# BUILTIN LIST List #-}
infixr 5 _∷_
The constructors are bound automatically when binding the type. Lists are not
required to be level polymorphic; List : Set → Set is also accepted.
As with booleans, the effect of binding the LIST built-in is to let
you use primitive functions working with lists, such as primStringToList
and primStringFromList, and letting the GHC backend
know to compile the List type to Haskell lists.
Maybe¶
module Agda.Builtin.Maybe
Built-in maybe type is bound using the MAYBE built-in:
data Maybe {a} (A : Set a) : Set a where
nothing : Maybe A
just : A → Maybe A
{-# BUILTIN MAYBE Maybe #-}
The constructors are bound automatically when binding the type. Maybe is not
required to be level polymorphic; Maybe : Set → Set is also accepted.
As with list, the effect of binding the MAYBE built-in is to let
you use primitive functions working with maybes, such as primStringUncons
that returns the head and tail of a string (if it is non empty), and letting
the GHC backend know to compile the Maybe type to Haskell
maybes.
Booleans¶
module Agda.Builtin.Bool where
Built-in booleans are bound using the BOOL, TRUE and FALSE built-ins:
data Bool : Set where
false true : Bool
{-# BUILTIN BOOL Bool #-}
{-# BUILTIN TRUE true #-}
{-# BUILTIN FALSE false #-}
Note that unlike for natural numbers, you need to bind the constructors separately. The reason for this is that Agda cannot tell which constructor should correspond to true and which to false, since you are free to name them whatever you like.
The effect of binding the boolean type is that you can then use primitive
functions returning booleans, such as built-in NATEQUALS, and letting the
GHC backend know to compile the type to Haskell Bool.
Natural numbers¶
module Agda.Builtin.Nat
Built-in natural numbers are bound using the NATURAL built-in as follows:
data Nat : Set where
zero : Nat
suc : Nat → Nat
{-# BUILTIN NATURAL Nat #-}
The names of the data type and the constructors can be chosen freely, but the shape of the datatype needs to match the one given above (modulo the order of the constructors). Note that the constructors need not be bound explicitly.
Binding the built-in natural numbers as above has the following effects:
- The use of natural number literals is
enabled. By default the type of a natural number literal will be
Nat, but it can be overloaded to include other types as well. - Closed natural numbers are represented as Haskell integers at compile-time.
- The compiler backends compile natural numbers to the appropriate number type in the target language.
- Enabled binding the built-in natural number functions described below.
Functions on natural numbers¶
There are a number of built-in functions on natural numbers. These are special in that they have both an Agda definition and a primitive implementation. The primitive implementation is used to evaluate applications to closed terms, and the Agda definition is used otherwise. This lets you prove things about the functions while still enjoying good performance of compile-time evaluation. The built-in functions are the following:
_+_ : Nat → Nat → Nat
zero + m = m
suc n + m = suc (n + m)
{-# BUILTIN NATPLUS _+_ #-}
_-_ : Nat → Nat → Nat
n - zero = n
zero - suc m = zero
suc n - suc m = n - m
{-# BUILTIN NATMINUS _-_ #-}
_*_ : Nat → Nat → Nat
zero * m = zero
suc n * m = (n * m) + m
{-# BUILTIN NATTIMES _*_ #-}
_==_ : Nat → Nat → Bool
zero == zero = true
suc n == suc m = n == m
_ == _ = false
{-# BUILTIN NATEQUALS _==_ #-}
_<_ : Nat → Nat → Bool
_ < zero = false
zero < suc _ = true
suc n < suc m = n < m
{-# BUILTIN NATLESS _<_ #-}
div-helper : Nat → Nat → Nat → Nat → Nat
div-helper k m zero j = k
div-helper k m (suc n) zero = div-helper (suc k) m n m
div-helper k m (suc n) (suc j) = div-helper k m n j
{-# BUILTIN NATDIVSUCAUX div-helper #-}
mod-helper : Nat → Nat → Nat → Nat → Nat
mod-helper k m zero j = k
mod-helper k m (suc n) zero = mod-helper 0 m n m
mod-helper k m (suc n) (suc j) = mod-helper (suc k) m n j
{-# BUILTIN NATMODSUCAUX mod-helper #-}
The Agda definitions are checked to make sure that they really define the corresponding built-in function. The definitions are not required to be exactly those given above, for instance, addition and multiplication can be defined by recursion on either argument, and you can swap the arguments to the addition in the recursive case of multiplication.
The NATDIVSUCAUX and NATMODSUCAUX are built-ins bind helper functions
for defining natural number division and modulo operations, and satisfy the
properties
div n (suc m) ≡ div-helper 0 m n m
mod n (suc m) ≡ mod-helper 0 m n m
Machine words¶
module Agda.Builtin.Word
module Agda.Builtin.Word.Properties
Agda supports built-in 64-bit machine words, bound with the WORD64 built-in:
postulate Word64 : Set
{-# BUILTIN WORD64 Word64 #-}
Machine words can be converted to and from natural numbers using the following primitives:
primitive
primWord64ToNat : Word64 → Nat
primWord64FromNat : Nat → Word64
Converting to a natural number is the trivial embedding, and converting from a natural number
gives you the remainder modulo 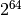 . The proof of the former theorem:
. The proof of the former theorem:
primitive
primWord64ToNatInjective : ∀ a b → primWord64ToNat a ≡ primWord64ToNat b → a ≡ b
is in the Properties module. The proof of the latter theorem is not primitive,
but can be defined in a library using primTrustMe.
Basic arithmetic operations can be defined on Word64 by converting to
natural numbers, performing the corresponding operation, and then converting
back. The compiler will optimise these to use 64-bit arithmetic. For
instance:
addWord : Word64 → Word64 → Word64
addWord a b = primWord64FromNat (primWord64ToNat a + primWord64ToNat b)
subWord : Word64 → Word64 → Word64
subWord a b = primWord64FromNat ((primWord64ToNat a + 18446744073709551616) - primWord64ToNat b)
These compile to primitive addition and subtraction on 64-bit words, which in the
GHC backend map to operations on Haskell 64-bit words
(Data.Word.Word64).
Integers¶
module Agda.Builtin.Int
Built-in integers are bound with the INTEGER built-in to a data type with
two constructors: one for positive and one for negative numbers. The built-ins
for the constructors are INTEGERPOS and INTEGERNEGSUC.
data Int : Set where
pos : Nat → Int
negsuc : Nat → Int
{-# BUILTIN INTEGER Int #-}
{-# BUILTIN INTEGERPOS pos #-}
{-# BUILTIN INTEGERNEGSUC negsuc #-}
Here negsuc n represents the integer -n - 1. Unlike for natural
numbers, there is no special representation of integers at compile-time since
the overhead of using the data type compared to Haskell integers is not that
big.
Built-in integers support the following primitive operation (given a suitable binding for String):
primitive
primShowInteger : Int → String
Floats¶
module Agda.Builtin.Float
module Agda.Builtin.Float.Properties
Floating point numbers are bound with the FLOAT built-in:
postulate Float : Set
{-# BUILTIN FLOAT Float #-}
This lets you use floating point literals. Floats are represented by the type checker as IEEE 754 binary64 double precision floats, with the restriction that there is exactly one NaN value. The following primitive functions are available (with suitable bindings for Nat, Bool, String, Int, Maybe_):
primitive
-- Relations
primFloatIsInfinite : Float → Bool
primFloatIsNaN : Float → Bool
primFloatIsNegativeZero : Float → Bool
-- Conversions
primNatToFloat : Nat → Float
primIntToFloat : Int → Float
primFloatToRatio : Float → (Σ Int λ _ → Int)
primRatioToFloat : Int → Int → Float
primShowFloat : Float → String
-- Operations
primFloatPlus : Float → Float → Float
primFloatMinus : Float → Float → Float
primFloatTimes : Float → Float → Float
primFloatDiv : Float → Float → Float
primFloatPow : Float → Float → Float
primFloatNegate : Float → Float
primFloatSqrt : Float → Float
primFloatExp : Float → Float
primFloatLog : Float → Float
primFloatSin : Float → Float
primFloatCos : Float → Float
primFloatTan : Float → Float
primFloatASin : Float → Float
primFloatACos : Float → Float
primFloatATan : Float → Float
primFloatATan2 : Float → Float → Float
primFloatSinh : Float → Float
primFloatCosh : Float → Float
primFloatTanh : Float → Float
primFloatASinh : Float → Float
primFloatACosh : Float → Float
primFloatATanh : Float → Float
The primitive binary relations implement their IEEE 754 equivalents, which means
that primFloatEquality is not reflexive, and primFloatInequality and
primFloatLess are not total. (Specifically, NaN is not related to anything,
including itself.)
The primFloatIsSafeInteger function determines whether the value is a number
that is a safe integer, i.e., is within the range where the arithmetic
operations do not lose precision.
Floating point numbers can be converted to their raw representation using the primitive:
primitive
primFloatToWord64 : Float → Word64
which normalises all NaN to a canonical NaN with an injectivity proof:
primFloatToWord64Injective : ∀ a b → primFloatToWord64 a ≡ primFloatToWord64 b → a ≡ b
in the Properties module. These primitives can be used to define a safe
decidable propositional equality with the --safe option. The function
primFloatToWord64 cannot be guaranteed to be consistent across backends,
therefore relying on the specific result may result in inconsistencies.
The rounding operations (primFloatRound, primFloatFloor, and
primFloatCeiling) return a value of type Maybe Int, and return nothing
when applied to NaN or the infinities:
primitive
primFloatRound : Float → Maybe Int
primFloatFloor : Float → Maybe Int
primFloatCeiling : Float → Maybe Int
The primFloatDecode function decodes a floating-point number to its mantissa
and exponent, normalised such that the mantissa is the smallest possible
integer. It fails when applied to NaN or the infinities, returning nothing.
The primFloatEncode function encodes a pair of a mantissa and exponent to a
floating-point number. It fails when the resulting number cannot be represented
as a float. Note that primFloatEncode may result in a loss of precision.
- primitive
- primFloatDecode : Float → Maybe (Σ Int λ _ → Int) primFloatEncode : Int → Int → Maybe Float
Characters¶
module Agda.Builtin.Char
module Agda.Builtin.Char.Properties
The character type is bound with the CHARACTER built-in:
postulate Char : Set
{-# BUILTIN CHAR Char #-}
Binding the character type lets you use character literals. The following primitive functions are available on characters (given suitable bindings for Bool, Nat and String):
primitive
primIsLower : Char → Bool
primIsDigit : Char → Bool
primIsAlpha : Char → Bool
primIsSpace : Char → Bool
primIsAscii : Char → Bool
primIsLatin1 : Char → Bool
primIsPrint : Char → Bool
primIsHexDigit : Char → Bool
primToUpper : Char → Char
primToLower : Char → Char
primCharToNat : Char → Nat
primNatToChar : Nat → Char
primShowChar : Char → String
These functions are implemented by the corresponding Haskell functions from
Data.Char (ord and chr for primCharToNat and
primNatToChar). To make primNatToChar total chr is applied to the
natural number modulo 0x110000. Furthermore, to match the behaviour of
strings, surrogate code points are mapped to the replacement
character U+FFFD.
Converting to a natural number is the obvious embedding, and its proof:
primitive
primCharToNatInjective : ∀ a b → primCharToNat a ≡ primCharToNat b → a ≡ b
can be found in the Properties module.
Strings¶
module Agda.Builtin.String
module Agda.Builtin.String.Properties
The string type is bound with the STRING built-in:
postulate String : Set
{-# BUILTIN STRING String #-}
Binding the string type lets you use string literals. The following primitive functions are available on strings (given suitable bindings for Bool, Char and List):
primitive
primStringUncons : String → Maybe (Σ Char (λ _ → String))
primStringToList : String → List Char
primStringFromList : List Char → String
primStringAppend : String → String → String
primStringEquality : String → String → Bool
primShowString : String → String
String literals can be overloaded.
Converting to and from a list is injective, and their proofs:
primitive
primStringToListInjective : ∀ a b → primStringToList a ≡ primStringToList b → a ≡ b
primStringFromListInjective : ∀ a b → primStringFromList a ≡ primStringFromList b → a ≡ b
can found in the Properties module.
Strings cannot represent unicode surrogate code points
(characters in the range U+D800 to U+DFFF). These are replaced by the
unicode replacement character U+FFFD if they appear in string literals.
Equality¶
module Agda.Builtin.Equality
The identity type can be bound to the built-in EQUALITY as follows
infix 4 _≡_
data _≡_ {a} {A : Set a} (x : A) : A → Set a where
refl : x ≡ x
{-# BUILTIN EQUALITY _≡_ #-}
This lets you use proofs of type lhs ≡ rhs in the rewrite
construction.
Other variants of the identity type are also accepted as built-in:
data _≡_ {A : Set} : (x y : A) → Set where
refl : (x : A) → x ≡ x
The type of primEraseEquality has to match the flavor of identity type.
module Agda.Builtin.Equality.Erase
Binding the built-in equality type also enables the primEraseEquality primitive:
primitive
primEraseEquality : ∀ {a} {A : Set a} {x y : A} → x ≡ y → x ≡ y
The function takes a proof of an equality between two values x and y and stays
stuck on it until x and y actually become definitionally equal. Whenever that
is the case, primEraseEquality e reduces to refl.
One use of primEraseEquality is to replace an equality proof computed using an expensive
function (e.g. a proof by reflection) by one which is trivially refl on the diagonal.
primTrustMe¶
module Agda.Builtin.TrustMe
From the primEraseEquality primitive, we can derive a notion of primTrustMe:
primTrustMe : ∀ {a} {A : Set a} {x y : A} → x ≡ y
primTrustMe {x = x} {y} = primEraseEquality unsafePrimTrustMe
where postulate unsafePrimTrustMe : x ≡ y
As can be seen from the type, primTrustMe must be used with the
utmost care to avoid inconsistencies. What makes it different from a
postulate is that if x and y are actually definitionally
equal, primTrustMe reduces to refl. One use of primTrustMe
is to lift the primitive boolean equality on built-in types like
String to something that returns a proof
object:
eqString : (a b : String) → Maybe (a ≡ b)
eqString a b = if primStringEquality a b
then just primTrustMe
else nothing
With this definition eqString "foo" "foo" computes to just refl.
Sorts¶
The primitive sorts used in Agda’s type system (Set, Prop, and
Setω) are declared using BUILTIN pragmas in the
Agda.Primitive module. These pragmas should not be used directly
in other modules, but it is possible to rename these builtin sorts
when importing Agda.Primitive.
{-# BUILTIN TYPE Set #-}
{-# BUILTIN PROP Prop #-}
{-# BUILTIN SETOMEGA Setω #-}
The primitive sorts Set and Prop are automatically imported at the
top of every top-level Agda module, unless the
--no-import-sorts flag is enabled.
Universe levels¶
module Agda.Primitive
Universe levels are also declared using BUILTIN
pragmas. In contrast to the Agda.Builtin modules, the Agda.Primitive module
is auto-imported and thus it is not possible to change the level built-ins. For
reference these are the bindings:
postulate
Level : Set
lzero : Level
lsuc : Level → Level
_⊔_ : Level → Level → Level
{-# BUILTIN LEVEL Level #-}
{-# BUILTIN LEVELZERO lzero #-}
{-# BUILTIN LEVELSUC lsuc #-}
{-# BUILTIN LEVELMAX _⊔_ #-}
Sized types¶
module Agda.Builtin.Size
The built-ins for sized types are different from other
built-ins in that the names are defined by the BUILTIN pragma. Hence, to
bind the size primitives it is enough to write:
{-# BUILTIN SIZEUNIV SizeUniv #-} -- SizeUniv : SizeUniv
{-# BUILTIN SIZE Size #-} -- Size : SizeUniv
{-# BUILTIN SIZELT Size<_ #-} -- Size<_ : ..Size → SizeUniv
{-# BUILTIN SIZESUC ↑_ #-} -- ↑_ : Size → Size
{-# BUILTIN SIZEINF ∞ #-} -- ∞ : Size
{-# BUILTIN SIZEMAX _⊔ˢ_ #-} -- _⊔ˢ_ : Size → Size → Size
Coinduction¶
module Agda.Builtin.Coinduction
The following built-ins are used for coinductive definitions:
postulate
∞ : ∀ {a} (A : Set a) → Set a
♯_ : ∀ {a} {A : Set a} → A → ∞ A
♭ : ∀ {a} {A : Set a} → ∞ A → A
{-# BUILTIN INFINITY ∞ #-}
{-# BUILTIN SHARP ♯_ #-}
{-# BUILTIN FLAT ♭ #-}
See Coinduction for more information.
IO¶
module Agda.Builtin.IO
The sole purpose of binding the built-in IO type is to let Agda check that
the main function has the right type (see Compilers).
postulate IO : Set → Set
{-# BUILTIN IO IO #-}
Literal overloading¶
module Agda.Builtin.FromNat
module Agda.Builtin.FromNeg
module Agda.Builtin.FromString
The machinery for overloading literals uses built-ins for the conversion functions.
Reflection¶
module Agda.Builtin.Reflection
The reflection machinery has built-in types for representing Agda programs. See Reflection for a detailed description.
Rewriting¶
The experimental and totally unsafe rewriting machinery (not
to be confused with the rewrite construct) has a built-in
REWRITE for the rewriting relation:
postulate _↦_ : ∀ {a} {A : Set a} → A → A → Set a
{-# BUILTIN REWRITE _↦_ #-}
This builtin is bound to the builtin equality type from Agda.Builtin.Equality in
Agda.Builtin.Equality.Rewrite.
Static values¶
The STATIC pragma can be used to mark definitions which should
be normalised before compilation. The typical use case for this is
to mark the interpreter of an embedded language as STATIC:
{-# STATIC <Name> #-}
Strictness¶
module Agda.Builtin.Strict
There are two primitives for controlling evaluation order:
primitive
primForce : ∀ {a b} {A : Set a} {B : A → Set b} (x : A) → (∀ x → B x) → B x
primForceLemma : ∀ {a b} {A : Set a} {B : A → Set b} (x : A) (f : ∀ x → B x) → primForce x f ≡ f x
where _≡_ is the built-in equality. At compile-time
primForce x f evaluates to f x when x is in weak head normal form (whnf),
i.e. one of the following:
- a constructor application
- a literal
- a lambda abstraction
- a type constructor application (data or record type)
- a function type
- a universe (
Set _)
Similarly primForceLemma x f, which lets you reason about programs using
primForce, evaluates to refl when x is in whnf. At run-time,
primForce e f is compiled (by the GHC backend)
to let x = e in seq x (f x).
For example, consider the following function:
-- pow’ n a = a 2ⁿ
pow’ : Nat → Nat → Nat
pow’ zero a = a
pow’ (suc n) a = pow’ n (a + a)
There is a space leak here (both for compile-time and run-time evaluation),
caused by unevaluated a + a thunks. This problem can be fixed with
primForce:
infixr 0 _$!_
_$!_ : ∀ {a b} {A : Set a} {B : A → Set b} → (∀ x → B x) → ∀ x → B x
f $! x = primForce x f
-- pow n a = a 2ⁿ
pow : Nat → Nat → Nat
pow zero a = a
pow (suc n) a = pow n $! a + a