With-Abstraction¶
With-abstraction was first introduced by Conor McBride [McBride2004] and lets you pattern match on the result of an intermediate computation by effectively adding an extra argument to the left-hand side of your function.
Usage¶
In the simplest case the with construct can be used just to discriminate on
the result of an intermediate computation. For instance
filter : {A : Set} → (A → Bool) → List A → List A
filter p [] = []
filter p (x ∷ xs) with p x
filter p (x ∷ xs) | true = x ∷ filter p xs
filter p (x ∷ xs) | false = filter p xs
The clause containing the with-abstraction has no right-hand side. Instead it
is followed by a number of clauses with an extra argument on the left,
separated from the original arguments by a vertical bar (|).
When the original arguments are the same in the new clauses you can use the
... syntax:
filter : {A : Set} → (A → Bool) → List A → List A
filter p [] = []
filter p (x ∷ xs) with p x
... | true = x ∷ filter p xs
... | false = filter p xs
In this case ... expands to filter p (x ∷ xs). There are three cases
where you have to spell out the left-hand side:
- If you want to do further pattern matching on the original arguments.
- When the pattern matching on the intermediate result refines some of the other arguments (see Dot patterns).
- To disambiguate the clauses of nested with-abstractions (see Nested with-abstractions below).
Generalisation¶
The power of with-abstraction comes from the fact that the goal type
and the type of the original arguments are generalised over the value
of the scrutinee. See Technical details below for the details.
This generalisation is important when you have to prove properties
about functions defined using with. For instance, suppose we want
to prove that the filter function above satisfies some property
P. Starting out by pattern matching of the list we get the
following (with the goal types shown in the holes)
postulate P : ∀ {A} → List A → Set
postulate p-nil : P []
postulate Q : Set
postulate q-nil : Q
proof : {A : Set} (p : A → Bool) (xs : List A) → P (filter p xs)
proof p [] = {! P [] !}
proof p (x ∷ xs) = {! P (filter p xs | p x) !}
In the cons case we have to prove that P holds for filter p xs | p x.
This is the syntax for a stuck with-abstraction—filter cannot reduce
since we don’t know the value of p x. This syntax is used for printing, but
is not accepted as valid Agda code. Now if we with-abstract over p x, but
don’t pattern match on the result we get:
proof : {A : Set} (p : A → Bool) (xs : List A) → P (filter p xs)
proof p [] = p-nil
proof p (x ∷ xs) with p x
... | r = {! P (filter p xs | r) !}
Here the p x in the goal type has been replaced by the variable r
introduced for the result of p x. If we pattern match on r the
with-clauses can reduce, giving us:
proof : {A : Set} (p : A → Bool) (xs : List A) → P (filter p xs)
proof p [] = p-nil
proof p (x ∷ xs) with p x
... | true = {! P (x ∷ filter p xs) !}
... | false = {! P (filter p xs) !}
Both the goal type and the types of the other arguments are generalised, so it
works just as well if we have an argument whose type contains filter p xs.
proof₂ : {A : Set} (p : A → Bool) (xs : List A) → P (filter p xs) → Q
proof₂ p [] _ = q-nil
proof₂ p (x ∷ xs) H with p x
... | true = {! H : P (filter p xs) !}
... | false = {! H : P (x ∷ filter p xs) !}
The generalisation is not limited to scrutinees in other with-abstractions. All occurrences of the term in the goal type and argument types will be generalised.
Note that this generalisation is not always type correct and may result in a (sometimes cryptic) type error. See Ill-typed with-abstractions below for more details.
Nested with-abstractions¶
With-abstractions can be nested arbitrarily. The only thing to keep in mind in
this case is that the ... syntax applies to the closest with-abstraction.
For example, suppose you want to use ... in the definition below.
compare : Nat → Nat → Comparison
compare x y with x < y
compare x y | false with y < x
compare x y | false | false = equal
compare x y | false | true = greater
compare x y | true = less
You might be tempted to replace compare x y with ... in all the
with-clauses as follows.
compare : Nat → Nat → Comparison
compare x y with x < y
... | false with y < x
... | false = equal
... | true = greater
... | true = less -- WRONG
This, however, would be wrong. In the last clause the ... is interpreted as
belonging to the inner with-abstraction (the whitespace is not taken into
account) and thus expands to compare x y | false | true. In this case you
have to spell out the left-hand side and write
compare : Nat → Nat → Comparison
compare x y with x < y
... | false with y < x
... | false = equal
... | true = greater
compare x y | true = less
Simultaneous abstraction¶
You can abstract over multiple terms in a single with-abstraction. To do this
you separate the terms with vertical bars (|).
compare : Nat → Nat → Comparison
compare x y with x < y | y < x
... | true | _ = less
... | _ | true = greater
... | false | false = equal
In this example the order of abstracted terms does not matter, but in general it does. Specifically, the types of later terms are generalised over the values of earlier terms. For instance
postulate plus-commute : (a b : Nat) → a + b ≡ b + a
postulate P : Nat → Set
thm : (a b : Nat) → P (a + b) → P (b + a)
thm a b t with a + b | plus-commute a b
thm a b t | ab | eq = {! t : P ab, eq : ab ≡ b + a !}
Note that both the type of t and the type of the result eq of
plus-commute a b have been generalised over a + b. If the terms in the
with-abstraction were flipped around, this would not be the case. If we now
pattern match on eq we get
thm : (a b : Nat) → P (a + b) → P (b + a)
thm a b t with a + b | plus-commute a b
thm a b t | .(b + a) | refl = {! t : P (b + a) !}
and can thus fill the hole with t. In effect we used the
commutativity proof to rewrite a + b to b + a in the type of
t. This is such a useful thing to do that there is special syntax
for it. See Rewrite below.
A limitation of generalisation is that only occurrences of the term that are
visible at the time of the abstraction are generalised over, but more instances
of the term may appear once you start filling in the right-hand side or do
further matching on the left. For instance, consider the following contrived
example where we need to match on the value of f n for the type of q to
reduce, but we then want to apply q to a lemma that talks about f n:
postulate
R : Set
P : Nat → Set
f : Nat → Nat
lemma : ∀ n → P (f n) → R
Q : Nat → Set
Q zero = ⊥
Q (suc n) = P (suc n)
proof : (n : Nat) → Q (f n) → R
proof n q with f n
proof n () | zero
proof n q | suc fn = {! q : P (suc fn) !}
Once we have generalised over f n we can no longer apply the lemma, which
needs an argument of type P (f n). To solve this problem we can add the
lemma to the with-abstraction:
proof : (n : Nat) → Q (f n) → R
proof n q with f n | lemma n
proof n () | zero | _
proof n q | suc fn | lem = lem q
In this case the type of lemma n (P (f n) → R) is generalised over f
n so in the right-hand side of the last clause we have q : P (suc fn) and
lem : P (suc fn) → R.
See The inspect idiom below for an alternative approach.
Using underscores and variables in pattern repetition¶
If an ellipsis … cannot be used, the with-clause has to repeat (or refine) the patterns of the parent clause. Since Agda 2.5.3, such patterns can be replaced by underscores _ if the variables they bind are not needed. Here is a (slightly contrived) example:
record R : Set where
coinductive -- disallows matching
field f : Bool
n : Nat
data P (r : R) : Nat → Set where
fTrue : R.f r ≡ true → P r zero
nSuc : P r (suc (R.n r))
data Q : (b : Bool) (n : Nat) → Set where
true! : Q true zero
suc! : ∀{b n} → Q b (suc n)
test : (r : R) {n : Nat} (p : P r n) → Q (R.f r) n
test r nSuc = suc!
test r (fTrue p) with R.f r
test _ (fTrue ()) | false
test _ _ | true = true! -- underscore instead of (isTrue _)
Since Agda 2.5.4, patterns can also be replaced by a variable:
f : List Nat → List Nat
f [] = []
f (x ∷ xs) with f xs
f xs0 | r = ?
The variable xs0 is treated as a let-bound variable with value .x ∷ .xs (where .x : Nat and .xs : List Nat are out of scope). Since with-abstraction may change the type of variables, the instantiation of such let-bound variables are type checked again after with-abstraction.
Irrefutable With¶
When a pattern is irrefutable, we can use a pattern-matching with
instead of a traditional with block. This gives us a lightweight
syntax to make a lot of observations before using a “proper” with
block. For a basic example of such an irrefutable pattern, see this
unfolding lemma for pred
pred : Nat → Nat
pred zero = zero
pred (suc n) = n
NotNull : Nat → Set
NotNull zero = ⊥ -- false
NotNull (suc n) = ⊤ -- trivially true
pred-correct : ∀ n (pr : NotNull n) → suc (pred n) ≡ n
pred-correct n pr with suc p ← n = refl
In the above code snippet we do not need to entertain the idea that n
could be equal to zero: Agda detects that the proof pr allows us
to dismiss such a case entirely.
The patterns used in such an inversion clause can be arbitrary. We can for instance have deep patterns, e.g. projecting out the second element of a vector whose length is neither 0 nor 1:
infixr 5 _∷_
data Vec {a} (A : Set a) : Nat → Set a where
[] : Vec A zero
_∷_ : ∀ {n} → A → Vec A n → Vec A (suc n)
second : ∀ {n} {pr : NotNull (pred n)} → Vec A n → A
second vs with (_ ∷ v ∷ _) ← vs = v
Remember example of simultaneous
abstraction from above. A simultaneous
rewrite / pattern-matching with is to be understood as being nested.
That is to say that the type refinements introduced by the first
case analysis may be necessary to type the following ones.
In the following example, in focusAt we are only able to perform
the splitAt we are interested in because we have massaged the type
of the vector argument using suc-+ first.
suc-+ : ∀ m n → suc m + n ≡ m + suc n
suc-+ zero n = refl
suc-+ (suc m) n rewrite suc-+ m n = refl
infixr 1 _×_
_×_ : ∀ {a b} (A : Set a) (B : Set b) → Set ?
A × B = Σ A (λ _ → B)
splitAt : ∀ m {n} → Vec A (m + n) → Vec A m × Vec A n
splitAt zero xs = ([] , xs)
splitAt (suc m) (x ∷ xs) with (ys , zs) ← splitAt m xs = (x ∷ ys , zs)
-- focusAt m (x₀ ∷ ⋯ ∷ xₘ₋₁ ∷ xₘ ∷ xₘ₊₁ ∷ ⋯ ∷ xₘ₊ₙ)
-- returns ((x₀ ∷ ⋯ ∷ xₘ₋₁) , xₘ , (xₘ₊₁ ∷ ⋯ ∷ xₘ₊ₙ))
focusAt : ∀ m {n} → Vec A (suc (m + n)) → Vec A m × A × Vec A n
focusAt m {n} vs rewrite suc-+ m n
with (before , focus ∷ after) ← splitAt m vs
= (before , focus , after)
You can alternate arbitrarily many rewrite and pattern-matching
with clauses and still perform a with abstraction afterwards
if necessary.
Rewrite¶
Remember example of simultaneous abstraction from above.
postulate plus-commute : (a b : Nat) → a + b ≡ b + a
thm : (a b : Nat) → P (a + b) → P (b + a)
thm a b t with a + b | plus-commute a b
thm a b t | .(b + a) | refl = t
This pattern of rewriting by an equation by with-abstracting over it and its left-hand side is common enough that there is special syntax for it:
thm : (a b : Nat) → P (a + b) → P (b + a)
thm a b t rewrite plus-commute a b = t
The rewrite construction takes a term eq of type lhs ≡ rhs, where _≡_
is the built-in equality type, and expands to a
with-abstraction of lhs and eq followed by a match of the result of
eq against refl:
f ps rewrite eq = v
-->
f ps with lhs | eq
... | .rhs | refl = v
One limitation of the rewrite construction is that you cannot do further
pattern matching on the arguments after the rewrite, since everything happens
in a single clause. You can however do with-abstractions after the rewrite. For
instance,
postulate T : Nat → Set
isEven : Nat → Bool
isEven zero = true
isEven (suc zero) = false
isEven (suc (suc n)) = isEven n
thm₁ : (a b : Nat) → T (a + b) → T (b + a)
thm₁ a b t rewrite plus-commute a b with isEven a
thm₁ a b t | true = t
thm₁ a b t | false = t
Note that the with-abstracted arguments introduced by the rewrite (lhs and
eq) are not visible in the code.
The inspect idiom¶
When you with-abstract a term t you lose the connection between
t and the new argument representing its value. That’s fine as long
as all instances of t that you care about get generalised by the
abstraction, but as we saw above this is not
always the case. In that example we used simultaneous abstraction to
make sure that we did capture all the instances we needed. An
alternative to that is to use the inspect idiom, which retains a
proof that the original term is equal to its abstraction.
In the simplest form, the inspect idiom uses a singleton type:
data Singleton {a} {A : Set a} (x : A) : Set a where
_with≡_ : (y : A) → x ≡ y → Singleton x
inspect : ∀ {a} {A : Set a} (x : A) → Singleton x
inspect x = x with≡ refl
Now instead of with-abstracting t, you can abstract over inspect t. For
instance,
filter : {A : Set} → (A → Bool) → List A → List A
filter p [] = []
filter p (x ∷ xs) with inspect (p x)
... | true with≡ eq = {! eq : p x ≡ true !}
... | false with≡ eq = {! eq : p x ≡ false !}
Here we get proofs that p x ≡ true and p x ≡ false in the respective
branches that we can use on the right. Note that since the with-abstraction is
over inspect (p x) rather than p x, the goal and argument types are no
longer generalised over p x. To fix that we can replace the singleton type
by a function graph type as follows (see Anonymous modules to learn
about the use of a module to bind the type arguments to Graph and
inspect):
module _ {a b} {A : Set a} {B : A → Set b} where
data Graph (f : ∀ x → B x) (x : A) (y : B x) : Set b where
ingraph : f x ≡ y → Graph f x y
inspect : (f : ∀ x → B x) (x : A) → Graph f x (f x)
inspect _ _ = ingraph refl
To use this on a term g v you with-abstract over both g v and inspect
g v. For instance, applying this to the example from above we get
postulate
R : Set
P : Nat → Set
f : Nat → Nat
lemma : ∀ n → P (f n) → R
Q : Nat → Set
Q zero = ⊥
Q (suc n) = P (suc n)
proof : (n : Nat) → Q (f n) → R
proof n q with f n | inspect f n
proof n () | zero | _
proof n q | suc fn | ingraph eq = {! q : P (suc fn), eq : f n ≡ suc fn !}
We could then use the proof that f n ≡ suc fn to apply lemma to q.
This version of the inspect idiom is defined (using slightly different names)
in the standard library in the module
Relation.Binary.PropositionalEquality and in the agda-prelude in
Prelude.Equality.Inspect (reexported by Prelude).
Alternatives to with-abstraction¶
Although with-abstraction is very powerful there are cases where you cannot or don’t want to use it. For instance, you cannot use with-abstraction if you are inside an expression in a right-hand side. In that case there are a couple of alternatives.
Pattern lambdas¶
Agda does not have a primitive case construct, but one can be emulated
using pattern matching lambdas. First you define a
function case_of_ as follows:
case_of_ : ∀ {a b} {A : Set a} {B : Set b} → A → (A → B) → B
case x of f = f x
You can then use this function with a pattern matching lambda as the second argument to get a Haskell-style case expression:
filter : {A : Set} → (A → Bool) → List A → List A
filter p [] = []
filter p (x ∷ xs) =
case p x of
λ { true → x ∷ filter p xs
; false → filter p xs
}
This version of case_of_ only works for non-dependent functions. For
dependent functions the target type will in most cases not be inferrable, but
you can use a variant with an explicit B for this case:
case_return_of_ : ∀ {a b} {A : Set a} (x : A) (B : A → Set b) → (∀ x → B x) → B x
case x return B of f = f x
The dependent version will let you generalise over the scrutinee, just like a with-abstraction, but you have to do it manually. Two things that it will not let you do is
- further pattern matching on arguments on the left-hand side, and
- refine arguments on the left by the patterns in the case expression. For
instance if you matched on a
Vec A nthenwould be refined by the nil and cons patterns.
Helper functions¶
Internally with-abstractions are translated to auxiliary functions
(see Technical details below) and you can always write these
functions manually. The downside is that the type signature for the
helper function needs to be written out explicitly, but fortunately
the Emacs Mode has a command (C-c C-h) to generate it using
the same algorithm that generates the type of a with-function.
Termination checking¶
The termination checker runs on the translated auxiliary functions, which
means that some code that looks like it should pass termination checking
does not. Specifically this happens in call chains like c₁ (c₂ x) ⟶ c₁ x
where the recursive call is under a with-abstraction. The reason is that
the auxiliary function only gets passed x, so the call chain is actually
c₁ (c₂ x) ⟶ x ⟶ c₁ x, and the termination checker cannot see that this
is terminating. For example:
data D : Set where
[_] : Nat → D
fails : D → Nat
fails [ zero ] = zero
fails [ suc n ] with some-stuff
... | _ = fails [ n ]
The easiest way to work around this problem is to perform a with-abstraction on the recursive call up front:
fixed : D → Nat
fixed [ zero ] = zero
fixed [ suc n ] with fixed [ n ] | some-stuff
... | rec | _ = rec
If the function takes more arguments you might need to abstract over a partial application to just the structurally recursive argument. For instance,
fails : Nat → D → Nat
fails _ [ zero ] = zero
fails _ [ suc n ] with some-stuff
... | m = fails m [ n ]
fixed : Nat → D → Nat
fixed _ [ zero ] = zero
fixed _ [ suc n ] with (λ m → fixed m [ n ]) | some-stuff
... | rec | m = rec m
A possible complication is that later with-abstractions might change the type of the abstracted recursive call:
T : D → Set
suc-T : ∀ {n} → T [ n ] → T [ suc n ]
zero-T : T [ zero ]
fails : (d : D) → T d
fails [ zero ] = zero-T
fails [ suc n ] with some-stuff
... | _ with [ n ]
... | z = suc-T (fails [ n ])
Trying to abstract over the recursive call as before does not work in this case.
still-fails : (d : D) → T d
still-fails [ zero ] = zero-T
still-fails [ suc n ] with still-fails [ n ] | some-stuff
... | rec | _ with [ n ]
... | z = suc-T rec -- Type error because rec : T z
To solve the problem you can add rec to the with-abstraction messing up
its type. This will prevent it from having its type changed:
fixed : (d : D) → T d
fixed [ zero ] = zero-T
fixed [ suc n ] with fixed [ n ] | some-stuff
... | rec | _ with rec | [ n ]
... | _ | z = suc-T rec
Performance considerations¶
The generalisation step of a with-abstraction needs to normalise the scrutinee and the goal and argument types to make sure that all instances of the scrutinee are generalised. The generalisation also needs to be type checked to make sure that it’s not ill-typed. This makes it expensive to type check a with-abstraction if
- the normalisation is expensive,
- the normalised form of the goal and argument types are big, making finding the instances of the scrutinee expensive,
- type checking the generalisation is expensive, because the types are big, or because checking them involves heavy computation.
In these cases it is worth looking at the alternatives to with-abstraction from above.
Technical details¶
Internally with-abstractions are translated to auxiliary functions—there are no with-abstractions in the Core language. This translation proceeds as follows. Given a with-abstraction
![\[\arraycolsep=1.4pt
\begin{array}{lrllcll}
\multicolumn{3}{l}{f : \Gamma \to B} \\
f ~ ps & \mathbf{with} ~ & t_1 & | & \ldots & | ~ t_m \\
f ~ ps_1 & | ~ & q_{11} & | & \ldots & | ~ q_{1m} &= v_1 \\
\vdots \\
f ~ ps_n & | ~ & q_{n1} & | & \ldots & | ~ q_{nm} &= v_n
\end{array}\]](../_images/math/bc5a4c4f2ab3b6f31135b81072c8ee46e045a642.png)
where 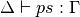 (i.e.
(i.e. 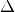 types the
variables bound in
types the
variables bound in 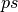 ), we
), we
Infer the types of the scrutinees
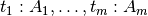 .
.Partition the context
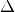 into
into 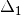 and
and
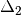 such that
such that 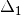 is the smallest context where
is the smallest context where
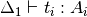 for all
for all 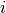 , i.e., where the scrutinees are well-typed.
Note that the partitioning is not required to be a split,
, i.e., where the scrutinees are well-typed.
Note that the partitioning is not required to be a split,
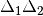 can be a (well-formed) reordering of
can be a (well-formed) reordering of 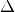 .
.Generalise over the
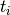 s, by computing
s, by computing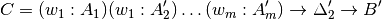
such that the normal form of
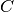 does not contain any
does not contain any 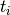 and
and![A_i'[w_1 := t_1 \ldots w_{i - 1} := t_{i - 1}] \simeq A_i
(\Delta_2' \to B')[w_1 := t_1 \ldots w_m := t_m] \simeq \Delta_2 \to B](../_images/math/986511ddfd9841cec3c6d7e6706057daf12a2a22.png)
where
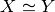 is equality of the normal forms of
is equality of the normal forms of 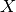 and
and
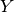 . The type of the auxiliary function is then
. The type of the auxiliary function is then 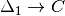 .
.Check that
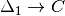 is type correct, which is not
guaranteed (see below).
is type correct, which is not
guaranteed (see below).Add a function
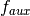 , mutually recursive with
, mutually recursive with 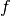 , with the
definition
, with the
definition![\[\arraycolsep=1.4pt
\begin{array}{llll}
\multicolumn{4}{l}{f_{aux} : \Delta_1 \to C} \\
f_{aux} ~ ps_{11} & \mathit{qs}_1 & ps_{21} &= v_1 \\
\vdots \\
f_{aux} ~ ps_{1n} & \mathit{qs}_n & ps_{2n} &= v_n \\
\end{array}\]](../_images/math/671f3f9e348925e8f14c843821957d4d69f80330.png)
where
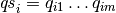 , and
, and 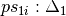 and
and
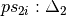 are the patterns from
are the patterns from 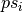 corresponding to
the variables of
corresponding to
the variables of 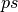 . Note that due to the possible reordering of the
partitioning of
. Note that due to the possible reordering of the
partitioning of 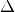 into
into 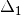 and
and 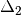 ,
the patterns
,
the patterns 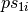 and
and 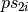 can be in a different order
from how they appear
can be in a different order
from how they appear 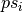 .
.Replace the with-abstraction by a call to
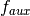 resulting in the
final definition
resulting in the
final definition![\[\arraycolsep=1.4pt
\begin{array}{l}
f : \Gamma \to B \\
f ~ ps = f_{aux} ~ \mathit{xs}_1 ~ ts ~ \mathit{xs}_2
\end{array}\]](../_images/math/d5682a814a0da4406ee2ad8a965d72d5bd0b899a.png)
where
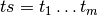 and
and 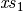 and
and
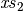 are the variables from
are the variables from 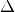 corresponding to
corresponding to
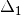 and
and 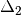 respectively.
respectively.
Examples¶
Below are some examples of with-abstractions and their translations.
postulate
A : Set
_+_ : A → A → A
T : A → Set
mkT : ∀ x → T x
P : ∀ x → T x → Set
-- the type A of the with argument has no free variables, so the with
-- argument will come first
f₁ : (x y : A) (t : T (x + y)) → T (x + y)
f₁ x y t with x + y
f₁ x y t | w = {!!}
-- Generated with function
f-aux₁ : (w : A) (x y : A) (t : T w) → T w
f-aux₁ w x y t = {!!}
-- x and p are not needed to type the with argument, so the context
-- is reordered with only y before the with argument
f₂ : (x y : A) (p : P y (mkT y)) → P y (mkT y)
f₂ x y p with mkT y
f₂ x y p | w = {!!}
f-aux₂ : (y : A) (w : T y) (x : A) (p : P y w) → P y w
f-aux₂ y w x p = {!!}
postulate
H : ∀ x y → T (x + y) → Set
-- Multiple with arguments are always inserted together, so in this case
-- t ends up on the left since it’s needed to type h and thus x + y isn’t
-- abstracted from the type of t
f₃ : (x y : A) (t : T (x + y)) (h : H x y t) → T (x + y)
f₃ x y t h with x + y | h
f₃ x y t h | w₁ | w₂ = {! t : T (x + y), goal : T w₁ !}
f-aux₃ : (x y : A) (t : T (x + y)) (h : H x y t) (w₁ : A) (w₂ : H x y t) → T w₁
f-aux₃ x y t h w₁ w₂ = {!!}
-- But earlier with arguments are abstracted from the types of later ones
f₄ : (x y : A) (t : T (x + y)) → T (x + y)
f₄ x y t with x + y | t
f₄ x y t | w₁ | w₂ = {! t : T (x + y), w₂ : T w₁, goal : T w₁ !}
f-aux₄ : (x y : A) (t : T (x + y)) (w₁ : A) (w₂ : T w₁) → T w₁
f-aux₄ x y t w₁ w₂ = {!!}
Ill-typed with-abstractions¶
As mentioned above, generalisation does not always produce well-typed results. This happens when you abstract over a term that appears in the type of a subterm of the goal or argument types. The simplest example is abstracting over the first component of a dependent pair. For instance,
postulate
A : Set
B : A → Set
H : (x : A) → B x → Set
bad-with : (p : Σ A B) → H (fst p) (snd p)
bad-with p with fst p
... | _ = {!!}
Here, generalising over fst p results in an ill-typed application H w
(snd p) and you get the following type error:
fst p != w of type A
when checking that the type (p : Σ A B) (w : A) → H w (snd p) of
the generated with function is well-formed
This message can be a little difficult to interpret since it only prints the
immediate problem (fst p != w) and the full type of the with-function. To
get a more informative error, pointing to the location in the type where the
error is, you can copy and paste the with-function type from the error message
and try to type check it separately.
| [McBride2004] | C. McBride and J. McKinna. The view from the left. Journal of Functional Programming, 2004. http://strictlypositive.org/vfl.pdf. |